homographie

homographie

homographie [ ɔmɔgrafi ] n. f.
• 1837; de homo- et -graphie
♦ Géom. Transformation ponctuelle bijective associée à une fonction homographique.
♢ Ling. Fait d'être homographe(s).

● homographie nom féminin Caractère des mots homographes. Isomorphisme entre espaces projectifs, défini à partir d'une application linéaire bijective entre les deux espaces vectoriels correspondants. ● homographie (expressions) nom féminin Homographie d'une conique C, bijection de C qui conserve le birapport. (Une telle homographie possède un axe.)

homographie
n. f. MATH Application qui transforme une droite d'un premier espace vectoriel en une droite d'un second.

I.
⇒HOMOGRAPHIE1, subst. fém.
LING. ,,Phénomène par lequel deux formes de même écriture (et souvent de même prononciation) ont des signifiés différents`` (Ling. 1972).
Prononc. : [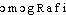]. Étymol. et Hist. 1906 ling. (Pt Lar.). Dér. de homographe; suff. -ie.
II.
⇒HOMOGRAPHIE2, subst. fém.
GÉOM. Transformation ponctuelle dans laquelle un point correspond à un point, une droite à une droite, un plan à un plan. [Deux figures homographiques sont telles] qu'à chaque point, à chaque droite, à chaque plan de l'une correspondent respectivement un point, une droite, un plan dans l'autre (...); et le principe en question sera dit principe de déformation homographique, ou simplement principe d'homographie (CHASLES, Aperçu hist. orig. et développ. méth. géom., 1837, p. 261). Le groupe fondamental est celui des homographies, c'est-à-dire celui des substitutions linéaires homogènes portant sur les coordonnées (Hist. gén. sc., t. 3, vol. 2, 1964, p. 77).
Prononc. : [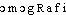]. Étymol. et Hist. 1837 géom. (CHASLES, loc. cit.). Composé de l'élém. homo- et de graphie.

homographie [ɔmɔgʀafi] n. f.
ÉTYM. 1837, Chasles; de homo-, et -graphie.
❖
♦ Géom. Transformation ponctuelle biunivoque définie par la fonction homographique.

Encyclopédie Universelle. 2012.

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Homographie — steht für: in der Linguistik ein Paar von Wörtern gleicher Schreibweise, aber unterschiedlicher Bedeutung, siehe Homograph in der Mathematik eine Kollineation des 2 dimensionalen reellen projektiven Raumes auf sich in der Stenografie für das von… …   Deutsch Wikipedia

  • Homographie — (griech.), s. Kollineation …   Meyers Großes Konversations-Lexikon

  • Homographie —   die, , Sprachwissenschaft: gleiche Schreibung von Wörtern unterschiedlicher Aussprache und Bedeutung, z. B. Tenor (als Bezeichnung für eine Stimmlage) und Tenor (als Bezeichnung für »Haltung«, »Inhalt«, »Sinn«, »Wortlaut«). Homophonie …   Universal-Lexikon

  • Homographie — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Homographie », sur le Wiktionnaire (dictionnaire universel) En linguistique, l homographie est un cas… …   Wikipédia en Français

  • homographie — (o mo gra fie) s. f. Terme de géométrie introduit par M. Chasles. Dépendance entre deux lignes telle qu à un point de l une correspond un point de l autre. Théorie de l homographie. ÉTYMOLOGIE    Homo...., et verbe grec signifiant tracer …   Dictionnaire de la Langue Française d'Émile Littré

  • Homographie d'une conique C — ● Homographie d une conique C bijection de C qui conserve le birapport. (Une telle homographie possède un axe.) …   Encyclopédie Universelle

  • Hétérographie — Homographie Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • Geometrie projective — Géométrie projective La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques …   Wikipédia en Français

  • Géométrie Projective — La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques 2 Aperçu élémentaire …   Wikipédia en Français

  • Géométrie projective — En mathématiques, la géométrie projective est le domaine de la géométrie qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés inchangées des figures par projection. Sommaire 1 Considérations historiques 2… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”